The Graceful Dance of Motion: Mass Attached to a Spring

The motion of a mass attached to a spring is a fascinating and essential concept in physics. It represents a classic example of simple harmonic motion (SHM), a fundamental behavior observed in countless natural phenomena. Whether it’s the bounce of a car’s suspension system, the sway of a pendulum, or the vibration of guitar strings, the motion of a mass connected to a spring reveals the elegance and predictability of nature’s rhythmic dance. In this article, we will explore the principles, equations, and real-world applications of this captivating phenomenon.

Understanding Mass-Spring Systems

A mass-spring system typically consists of two primary components:

1. Mass (m): The object or particle that is attached to the spring. Its inertia and mass determine how it responds to external forces.
2. Spring (k): A flexible, coiled structure that exerts a restoring force on the attached mass when it is displaced from its equilibrium position. The stiffness of the spring, often represented by the spring constant (k), influences the system’s behavior.

Characteristics of Mass-Spring Systems

To understand the motion of a mass attached to a spring, several key characteristics must be considered:

1. Equilibrium Position: The central, unperturbed position where the mass remains at rest when no external forces act on it. In this position, the spring is neither compressed nor extended.
2. Displacement (x): The distance the mass moves from its equilibrium position. A positive displacement indicates the mass has been stretched or extended, while a negative displacement indicates compression.
3. Restoring Force (F): The spring exerts a force proportional to the displacement of the mass from its equilibrium position. This restoring force is described by Hooke’s Law:F = – kx

   Where:

   • F is the restoring force.
   • k is the spring constant.
   • x is the displacement from the equilibrium position.
4. Simple Harmonic Motion (SHM): When a mass attached to a spring is displaced and released, it undergoes SHM. This means it oscillates back and forth around the equilibrium position, following a sinusoidal pattern.

Mathematical Representation

The motion of a mass-spring system can be described mathematically by the following equation:

Where:

• m is the mass of the object.
• d2x/dt2 represents the second derivative of displacement with respect to time, which describes acceleration.
• k is the spring constant.
• x is the displacement from the equilibrium position.
• The equation represents Newton’s second law of motion and Hooke’s Law.

Solving this differential equation yields a solution that describes the displacement as a function of time, which typically results in sinusoidal motion:

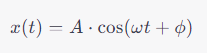
Where:

• x(t) is the displacement of the mass at time t.
• A is the amplitude of the motion.
• $\omega$ (omega) is the angular frequency, given by
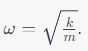
• $\varphi$ is the phase angle, determining the initial position of the mass in its oscillatory cycle.

Applications of Mass-Spring Systems

The motion of masses attached to springs finds applications in various fields:

1. Automotive Suspension: Vehicle suspensions employ springs to provide a smoother ride and improve handling by absorbing shocks and vibrations.
2. Mechanical Watches: The oscillation of a balance wheel, often with a hairspring, regulates the timekeeping in mechanical watches.
3. Seismology: Springs and mass systems are used in seismometers to detect and measure ground movements during earthquakes.
4. Structural Engineering: Mass-spring models are employed to analyze and mitigate vibrations in buildings and bridges.

Conclusion

The motion of a mass attached to a spring serves as a captivating illustration of the principles of simple harmonic motion and Hooke’s Law. This fundamental concept transcends the boundaries of physics, finding applications in engineering, automotive design, horology, and seismology. Through the graceful dance of oscillation, this phenomenon offers valuable insights into the beauty and order that underlie the natural world’s rhythmic motions.